Chongfan Technology

News

All Categories >

Home page

2025

Integrated Optical High-Dimensional Non-Abelian Geometric Phase

Author:

Non-Abelian geometric phase is a matrix-valued geometric phase generated by the cyclic evolution of quantum or classical systems in parameter space. In fundamental science, it can be used to analogously simulate the interactions of fundamental particles or explore theories beyond the Standard Model; in applications, it provides a fault-tolerant quantum gate implementation scheme for quantum computing and can also realize robust analog computing in classical wave systems. Therefore, achieving high-dimensional, universal non-Abelian geometric phases and functional devices has become a recent research hotspot.

Professor Su Yikai and Professor Guo Xuhan's research group and collaborative team from the School of Integrated Circuits (School of Information and Electronics Engineering), Shanghai Jiao Tong University The generation of arbitrary high-dimensional special orthogonal group (SO(m)) non-Abelian geometric phases was realized for the first time on a bilayer silicon nitride platform. This research fully utilized the ultra-compact characteristics of the integrated platform and the intrinsic robustness of geometric phases, successfully developing broadband (≥100 nm), high-order (≥6th order), and high-fidelity (>0.95) unitary matrix transformation devices. In addition to classical optical experiments, the work also realized quantum experiments with predicted single-photon state injection, further verifying the potential of non-Abelian geometric phases in classical optical computing and quantum optical computing fields. The related results were published under the title " High-dimensional non-Abelian holonomy in integrated photonics " (High-dimensional non-Abelian geometric phase in integrated optics) in Nature Communications . Chen Youlüe, a PhD student from the School of Integrated Circuits (School of Information and Electronics Engineering), Shanghai Jiao Tong University, is the first author. The corresponding authors are Professor Guo Xuhan and Professor Su Yikai from the School of Integrated Circuits (School of Information and Electronics Engineering), Shanghai Jiao Tong University, and Professor Zhang Xulin from Jilin University. This work was supported and guided by Professor Ma Guancong from Hong Kong Baptist University, Academician Guo Guangcan, Professor Zhou Qiang, and Associate Researcher Fan Yunru from the University of Electronic Science and Technology of China. Gulliver Larsonneur, a master's student from École Centrale de Lyon/Shanghai Jiao Tong University, postdoctoral researchers Xiang Jinlong and He An from Shanghai Jiao Tong University, and Dr. Wang Guohuai from Jilin University also made important contributions to this work.

When a quantum or classical system undergoes a cyclic evolution in parameter space, its final state acquires not only a dynamical phase determined by energy and time but also a geometric phase that depends solely on the geometric shape of the evolution path in parameter space (such as the solid angle enclosed) and is independent of the evolution time, thus possessing unique robustness. A famous example is the Pancharatnam-Berry phase, a scalar one-dimensional geometric phase. Building on this, F. Wilczek and A. Zee further proposed that when the system has degenerate energy levels, the adiabatic evolution of multiple degenerate states can produce a non-Abelian geometric phase. This type of geometric phase appears in matrix form, belonging to the high-dimensional unitary group U(m) (m>1), exhibiting non-commutativity, hence called non-Abelian geometric phase. In fundamental science, it can be used to construct artificial non-Abelian gauge fields, analogously simulate interactions of fundamental particles in the Standard Model, or explore theories beyond the Standard Model such as topological quantum field theory; in applications, geometric-phase-based all-geometric quantum operations have inherent noise resistance and are considered important candidates for fault-tolerant quantum computing. To date, non-Abelian geometric phases have been realized in various quantum platforms for quantum logic gates, such as cold atom systems, superconducting quantum circuits, ion traps, NV centers, etc. Recently, this originally quantum concept has gradually expanded to classical wave systems. Utilizing the rich intrinsic degrees of freedom in optical and acoustic waves, researchers have constructed artificial gauge fields in classical systems and observed non-Abelian geometric effects. This not only provides a new platform for exploring fundamental physics and opens an interdisciplinary frontier direction of "simulating quantum phenomena with classical systems," but also offers new ideas for designing broadband, interference-resistant, and highly robust devices based on geometric phase principles at the application level.

The research team constructed a high-dimensional non-Abelian geometric phase for the first time based on a bilayer silicon nitride waveguide integrated platform. As shown in Figure 1, this four-waveguide structure supports two degenerate supermodes. By precisely controlling the spacing between waveguides, the coupling coefficients can be continuously adjusted, driving the system to undergo adiabatic evolution in parameter space. When the system completes a cyclic evolution along a closed path, a basic SO(2) geometric phase unit is generated, where the input-output satisfies a linear relation of a second-order unitary matrix (belonging to the SO(2) group). By changing the parameters of the evolution path, general SO(2) matrix transformation devices can be realized ( Figure 1a ), as well as simulated arbitrary anyon-exchange two-mode braiding devices ( Figure 1b ).

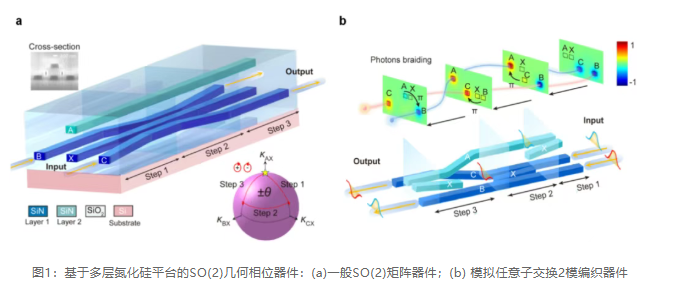
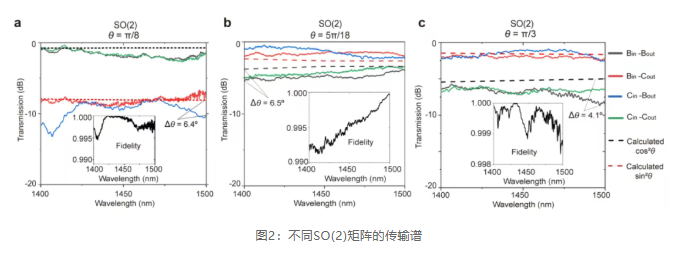
Figure 2 's transmission spectrum shows that the realized optical transformation maintains high fidelity over a broadband range exceeding 100 nm, demonstrating excellent broadband response characteristics. This advantage stems from the intrinsic property of the geometric phase—determined by the evolution path in parameter space, thus naturally robust against wavelength variations.

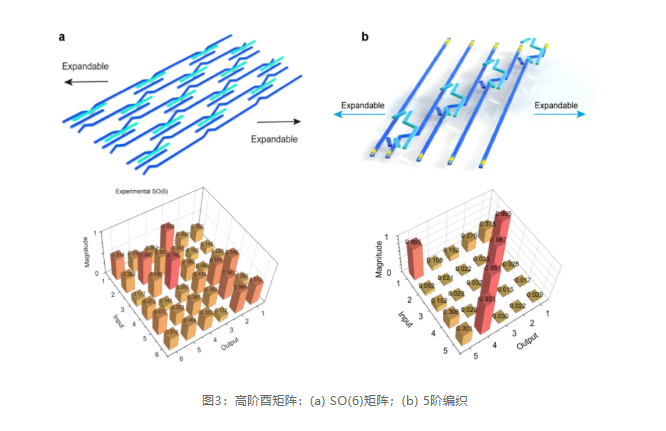
The SO(2) matrix describes rotation operations in a two-dimensional plane. Although the structure is simple, it forms the "basic building blocks" of high-dimensional orthogonal transformations. According to the Givens rotation principle—that any high-dimensional orthogonal matrix in the SO(m) group can be decomposed into a series of SO(2) basic units. The research team cascaded multiple SO(2) units based on non-Abelian geometric phases into an array, successfully realizing arbitrary dimensional SO(m) matrices. As shown in Figure 3 , the system experimentally demonstrated transformations up to 6th order (SO(6)) with transformation fidelity greater than 0.95. This increases the system's complexity and functional diversity, enabling more complex tasks. For example, in performing high-order matrix operations, SO(m) matrices provide a larger operational space capable of handling high-dimensional vectors. More importantly, thanks to the intrinsic properties of geometric phases, high-order transformations still maintain excellent broadband response. The realized 6th-order matrix operates stably over a wavelength range exceeding 50 nm, demonstrating robustness to wavelength variations. This broadband advantage opens new paths for parallel optical computing: combined with wavelength-division multiplexing (WDM) technology, multiple wavelength channels' data can be processed simultaneously on the same architecture, significantly improving system data throughput and energy efficiency, suitable for future high-speed optical interconnects and intelligent photonic processors.

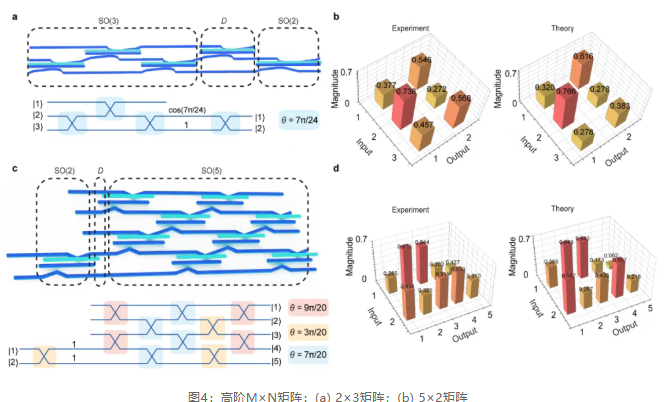
Additionally, based on the singular value decomposition model, the research team extended the SO(m) architecture to realize optical computing functions for arbitrary M×N matrices ( Figure 4 ). This generalized matrix transformation device also inherits broadband characteristics and can carry out computational tasks such as matrix-vector multiplication. This proof-of-concept demonstrates the potential of non-Abelian geometric phases in optical computing for matrix-vector multiplication to handle complex tasks.