Chongfan Technology
News
20
2025
-
08
Intrinsic Higher-Order Topological Insulators Based on Equivalent Medium Systems
Author:
Recently, Fudan University Future Information Innovation Institute's Young Researcher Shaojie Ma, Professor Zhou Lei from the Department of Physics, and Professor Zhang Shuang from the Department of Physics at the University of Hong Kong cooperated to achieve breakthrough progress in the field of topological state research, proving for the first time at both theoretical and experimental levels: intrinsic higher-order topological insulators (HOTI) exist in uniform electromagnetic media. The research found that when uniform electromagnetic media has a non-trivial second Chern number in synthetic high-dimensional space c 2 , any cross-sectional shape of the cylindrical structure formed exhibits topologically protected HOTI-type edge states. The uniqueness of this edge state lies in its intrinsic topological properties: its existence is completely independent of specific material parameters, geometric configurations, and system symmetries, revealing a new mechanism for realizing higher-order topological states. It is particularly noteworthy that this research differs from traditional HOTI, which is mainly based on tight-binding model theoretical frameworks, and for the first time realizes HOTI states in uniform equivalent medium systems, opening up new experimental platforms for the study of higher-order topological states.
Unlike conventional topological systems, higher-order topological insulators (HOTI) no longer follow the topological bulk-boundary correspondence where the bulk and boundary dimensions differ by one. For example, in three-dimensional systems, conventional topological states manifest as two-dimensional surface states, while HOTI can appear in regions where the dimensional difference between the bulk and boundary is greater, such as localized one-dimensional line-localized edge modes or even zero-dimensional corner-localized modes. Currently, most HOTI research focuses on discrete systems described by tight-binding models, such as electronic systems, topological circuits, and phononic crystals. However, whether similar higher-order topological modes exist in continuous metamaterial systems described by uniform equivalent medium models remains an unresolved question.
This paper confirms at both theoretical and experimental levels that HOTI-type edge states exist in uniform Yang monopole medium columns, as shown in Figure 1. These edge states arise from the non-trivial second Chern number in synthetic high-dimensional physical space. c 2 Its topological properties ensure the existence of edge modes. Specifically, the non-trivial c 2 topologically guarantees the existence of non-trivial boundary states with high-dimensional Weyl arc structures on the boundary, with Yang monopoles or Weyl surfaces having opposite second Chern numbers, where arcs connecting their projections exist on the boundary, and each point on the arc corresponds to a topological Weyl point in the synthetic space. The interaction between these Weyl points on the boundary arc and the effective magnetic field induced by the change in the normal direction of the cylindrical structure's boundary generates localized chiral zero modes, whose field distribution manifests as localized HOTI-type edge modes. Unlike traditional HOTI that relies on symmetry protection, this mechanism produces intrinsic higher-order topological modes, whose existence does not depend on specific material parameters, geometric configurations, or system symmetries, and can thus be universally realized in cylindrical structures of any cross-sectional shape and a series of uniform electromagnetic materials.
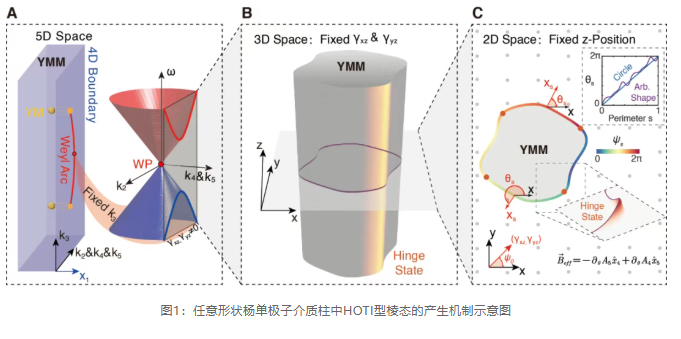
The research first starts from the topological surface characteristics of the Yang monopole equivalent medium, with the topologically non-trivial second Chern number c 2 , whose bulk-boundary correspondence is reflected in the existence of three-dimensional Fermi super surfaces and one-dimensional Weyl arcs on the four-dimensional boundary, as shown in Figure 1(a). In three-dimensional laboratory space, when the condition | k z | < k YM , the topological invariants guarantee the existence of intersection points of boundary states at the interface between the medium column and air. In synthetic high-dimensional space, these intersection points correspond to synthetic Weyl points with non-trivial first Chern numbers. c 2 For surfaces with normals along the x direction, given c 1 , its surface Hamiltonian can be analytically derived using the k·p approximation method: k z This Weyl-type Hamiltonian clearly reveals that the surface states inherit the intrinsic topological structure of the high-dimensional c. Furthermore, on the horizontal cross-section of any cylindrical structure, the closed nature of the boundary ensures that the normal direction of its profile continuously changes along the perimeter for a complete 2π cycle, as shown in Figure 1(c).
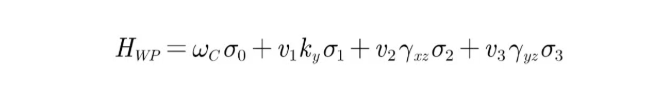
The research team first pointed out theoretically that due to the change in the normal direction, the angle between the material crystal axis and the interface normal direction varies along the perimeter. This relative rotation can be viewed as an artificial gauge potential, and the geometric curvature is thus equivalent to an artificial gauge field. This gauge field couples with the surface Weyl points, inducing the generation of topologically protected chiral zero modes. The field distribution of this mode presents an Hermitian Gaussian distribution along specific edge angles, localized overall on the side of the cylinder, forming a typical HOTI-type edge state, 2 as shown in Figure 1(b). The research team conducted theoretical calculations on the energy bands and field distribution characteristics of the cylindrical structure using different schemes such as finite element simulation, global plane wave expansion, and localized gauge field approximation, with results as shown in Figure 2. c 1 The results obtained from different schemes exhibit a high degree of consistency. It is worth emphasizing that the cylindrical geometric structure itself does not possess anisotropic characteristics; the topological edge state mode entirely originates from the inherent intrinsic topological properties of the electromagnetic medium. To further validate the theoretical predictions, the research team designed a metamaterial sample composed of metallic helical structural units to achieve the special electromagnetic equivalent medium response of synthetic high-dimensional Yang monopole media, and used finite element methods to simulate and analyze the energy band structure and field distribution characteristics of the cylindrical structure under square cross-section configurations, as shown in Figure 3(a-c).
The results show that in the band gap of the boundary states, there exists an independent HOTI mode, whose field distribution characteristics are highly localized in the lower right corner of the cross-section, clearly demonstrating its higher-order topological features. In terms of experiments, the research team prepared the corresponding samples based on printed circuit board technology and used a near-field scanning system to experimentally characterize the dispersion relations and field distribution characteristics, as shown in Figure 3(d-f).
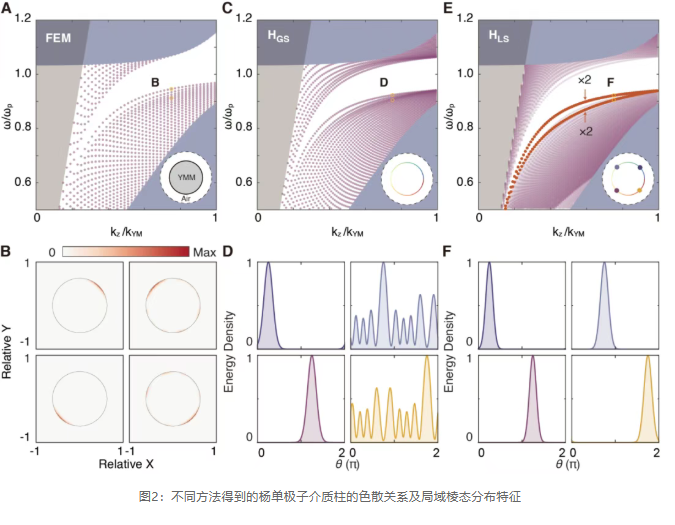
为进一步验证理论预测，研究团队设计了一种由金属螺旋结构单元构成的超构材料样品，用以实现合成高维空间杨单极子介质的特殊电磁等效媒质响应，并采用有限元法模拟分析了方型截面构型下柱结构的能带结构及场分布特征，如图3(a-c)所示。结果显示，在边界态的带隙中，存在独立的HOTI模式，其场分布特征高度局域于截面的右下角，清晰展现了其高阶拓扑特征。
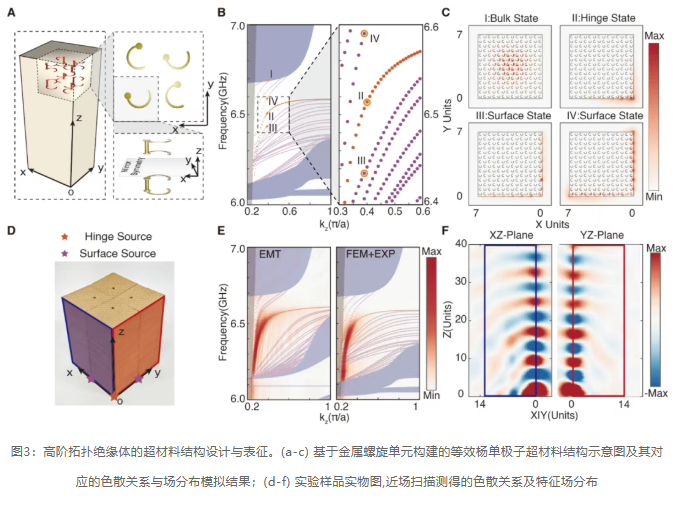
实验方面，研究团队基于印刷电路板技术制备了相应样品，并采用近场扫描系统对色散关系和场分布特征进行了实验表征，如图3(d-f) As shown. The experimental results clearly observed the dispersion relation of the edge modes within the band gap, and their localized distribution along the z-axis at specific frequencies. The results are highly consistent with the predictions of the equivalent medium theoretical model and full-wave simulations, systematically validating the feasibility of realizing higher-order topological insulators in a uniform equivalent medium system.
Summary and Outlook
This work utilizes the intrinsic properties of artificial atoms in the electromagnetic metamaterial platform to construct a new type of higher-order topological insulator, and experimentally verifies the existence of topological edge states in a uniform Yang monopole metamaterial cylinder with a square cross-section. 2 The non-trivial second Chern number c guarantees that the synthetic Weyl points naturally arise on the surface of the Yang monopole medium, while the inevitable curvature of the cylinder's side boundaries is equivalent to an external magnetic field, thereby inducing topological zero-energy modes localized along the edges. This mechanism cannot be explained by quantized dipole or multipole moments, nor is it similar to real Chern insulators protected by time-reversal symmetry, providing a new approach to achieving higher-order topological insulators. The research further highlights the strong potential and wide applicability of exploring novel topological effects by manipulating the constitutive relations of metamaterials.
LATEST NEWS
2025-08-20
High-order vortex beams assist super-resolution imaging
Recently, Professor Huang Zhiwei from the Department of Biomedical Engineering at the National University of Singapore led a biophotonics team in a latest study proposing that by introducing higher-order vortex beams into the minimal light flux (MINFLUX) imaging technology, the measurement accuracy of the imaging system can be significantly improved, thereby further breaking through the resolution limits of traditional optical imaging.
2025-08-20
Intrinsic Higher-Order Topological Insulators Based on Equivalent Medium Systems
Recently, Dr. Shaojie Ma, a young researcher at the Fudan University Institute of Future Information Innovation, Professor Lei Zhou from the Department of Physics, and Professor Shuang Zhang from the Department of Physics at the University of Hong Kong collaborated to achieve breakthrough progress in the field of topological state research, proving for the first time at both theoretical and experimental levels that intrinsic higher-order topological insulators (HOTI) exist in uniform electromagnetic media.
2025-08-20
Research on Non-Hermitian Properties Assisted by Orbital Angular Momentum Synthesis Dimensions
In quantum mechanics, observables usually need to satisfy Hermiticity to ensure that their eigenvalues are real numbers.
2025-08-20
Differentiable imaging unlocks full-link optimization
In the field of computational imaging, uncertainty has long constrained technological development.
2025-08-20
Reconfigurable multifunctional integrated optical computing chip
The development of artificial intelligence is driving the evolution of computing architecture towards higher performance, lower power consumption, and greater adaptability.
Thank you for visiting the official website of Chongfan Technology. If you have cooperation intentions or suggestions, please contact us through the following methods, and we will reply as soon as possible, thank you!
Address: Room 403, Building 6, Phase III of R&D, No. 36 Xiyong Avenue, High tech Zone, Chongqing, China.
Telephone: +86-13658337211
E-mail: Sales@cfkeji.net
Website: www.cfkeji.net
Mobile Version
